W arsenale Data Scientista znajduje się wiele modeli, za pomocą których może dokonywać regresji czy klasyfikacji. Drzewa losowe, ARMA, sieci neuronowe, regresja liniowa i wiele innych. Oczywiście, każdy z nich ma swoje wady i zalety, które często przeplatają się w taki sposób, że w zależności od postawionego problemu mogą zmienić rubryczkę na przeciwną. Dzisiaj przyjrzymy się wpływowi ilości danych na jakość działania i czas uczenia wybranych sieci neuronowych w porównaniu do innych modeli.

Wstęp

Nie muszą chyba zbyt długo przekonywać, że wpływ ilości dostępnych danych na wybór modelu, który ma być na nich uczony, jest ważną kwestią. Jeśli rozpoczniesz karierę w Data Science nie raz przyjdzie ci zmierzyć się z niewielkim zbiorem danych lub wręcz przeciwnie z ich natłokiem. Pomocą służyć może na przykład dobry feature engeenering, lub dostrojenie hipermarametrów modelu, okazuje się jednak, że modele czy całe ich klasy mają pewne wbudowane w swoje działanie właściwości. Sprawdźmy to!

Klasyfikacja

Rozpoznawania cyfr ze zbioru MNIST stało się odpowiednikiem “Hello World!” w świecie sieci neuronowych. MNIST to zbiór kilkudziesięciu tysięcy czarno-białych obrazków ręcznie pisanych cyfr od 0 do 9. Zadanie polega na właściwym odczytaniu cyfr przez algorytm.

Wybrane elementy zbioru MNIST

Zanim przystąpimy do wyboru modeli ustalmy jak będziemy porównywać ich skuteczność. Jako miarę wybieramy accuracy czyli ilość poprawnie rozpoznanych cyfr podzielona przez ilość wszystkich pokazanych cyfr podczas procesu testowania. Więcej na ten temat możecie przeczytać w artykule Co to znaczy dobrze? Ocena jakości modelu.

W pojedynku zmierzą się dwa algorytmy reprezentujące dwa różne, pod wieloma względami, nurty: Random Forest oraz konwolucyjna sieć neuronowa. Spośród wielu różnic najważniejszą będzie to, że sieć konwolucyjna należy do alorytmów tak zwanego uczenia głębokiego czyli sieci neuronowych mających co najmniej kilka warstw. Co do minimalnej ilości warstw aby sieć nazwać “głęboką” nie ma ogólnej zgody.

Wykres 1.1 ilustruje typowe zachowanie wspomnianych algorytmów. Standardowe algorytmy ML takie jak Random Forest szybciej osiągają nasycenie danymi. Oznacza to, że od pewnego momentu podanie większej ilości danych nie polepsza działania klasyfikatora. Przeważnie wymagają jednak mniejszej ilości danych do osiągnięcia rozsądnych rezultatów w porównaniu do metod deep learningu. Uczenie głębokie, którego przykładem jest sieć konwolucyjna potrzebuje zazwyczaj znacznie większej ilości danych do nauki. Jednak po ich dostarczeniu często uzyskują lepsze rezultaty niż “klasyczne” algorytmy ML. Nie ulegają one tak łatwemu ustabilizowaniu na jednym poziomie dokładności, lecz zwiększając liczbę danych jesteśmy w stanie polepszyć ich działanie. Jest to o tyle ważne, że wraz ze zbieraniem większej ilości danych możemy douczać model. W trakcie doświadczenia nie zmienialiśmy żadnego z hiperparametrów obu modeli.

Zwróćmy uwagę na rosnący liniowo czas potrzebny do nauczenia algorytmu. Las losowy pomimo podobnego czasu poświęconego na naukę od pewnego momentu nie polepsza swoich własności.

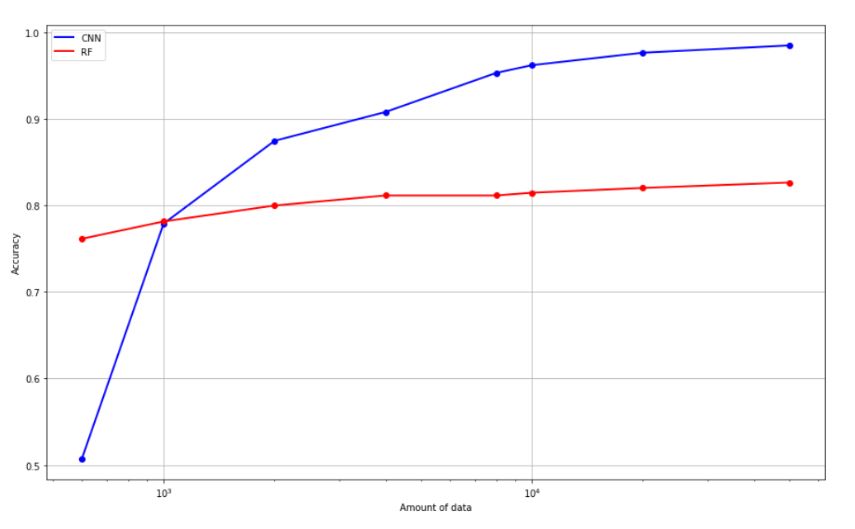
1.1 Jakość klasyfikacji w funkcji ilości danych uczących (pokazywanych algorytmowi unikalnych obrazów)

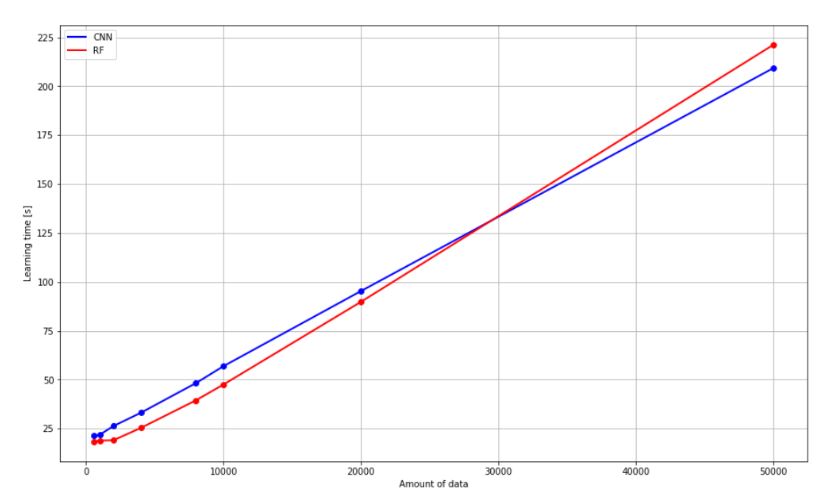
1.2 Czas uczenia algorytmów w funkcji ilości danych uczących (pokazywanych algorytmowi unikalnych obrazów)

Regresja

Drugi przykład ilustruje zagadnienie regresji. Na podstawie wybranych próbek z krzywej 2.1 model powinien nauczyć się wyznaczać wartość koordynatu Y dla zadanego X.

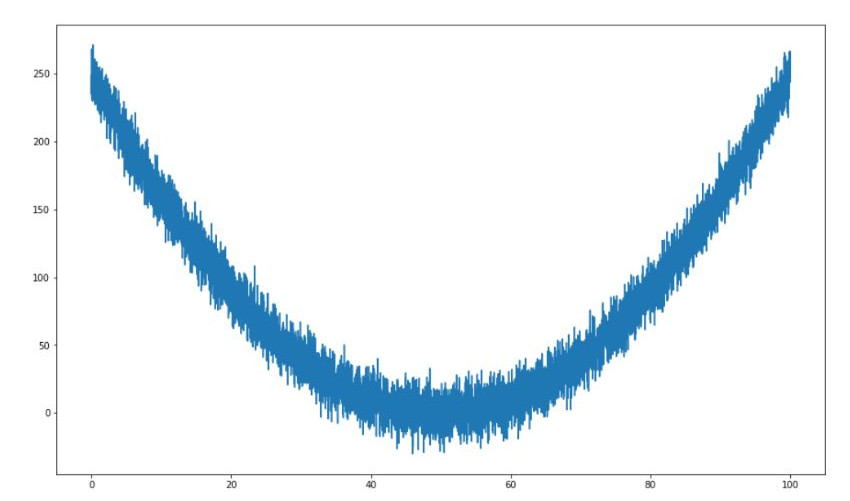
2.1 Zaszumiona krzywa drugiego stopnia

Również to zadanie rozpocznijmy od wyboru kryterium oceny modeli. Typowo w przypadku regresji jest to RMSE, czyli pierwiastek z sumy kwadratów różnic pomiędzy wartością rzeczywistą a estymowaną podzieloną przez ilość danych.

Tym razem wykorzystamy Lasso Regresji (LR) oraz sieć neuronową typu MLP. Proponowana sieć jest tak zwaną “siecią płytką”. Oznacza to, że składa się jedynie z warstwy wejściowej, ukrytej i wyjściowej, w przeciwieństwie do sieci głębokich mających kilka warstw ukrytych. Pomimo tak prostej architektury i niewielkiej ilości użytych neuronów generuje to sporą liczbę wag do dobrania w procesie uczenia.

Z uwagi na niewielki stopień trudności problemu prosty model regresyjny szybciej niż sieć i równie dobrze jak ona nauczył się estymować zadaną krzywą - wykres 2.2. Przewagą sieci jest jednak możliwość radzenia sobie z bardziej skomplikowanymi zależnościami. Po raz kolejny kluczową kwestią okazała się liczba potrzebnych dla sieci danych. Z uwagi na znacznie większą ilość parametrów, których wartości zmieniają się w trakcie procesu uczenia potrzebna jest także większa liczba danych. Kolejnym kosztem za zwiększenie potencjału estymacji poprzez użycie sieci jest zwiększenie złożoności uczenia z O(1) do O(n).

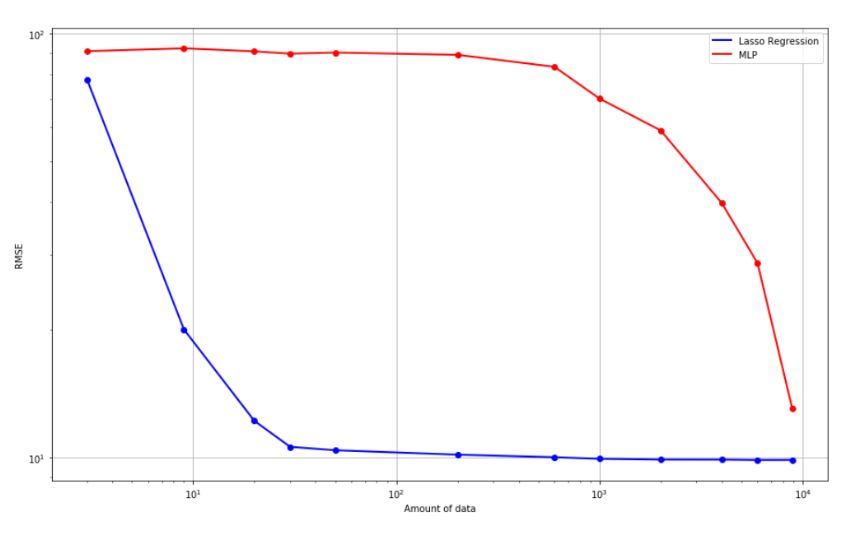
2.2 RMSE w funkcji ilości danych uczących (pokazywanych punktów z wykresu 2.1)

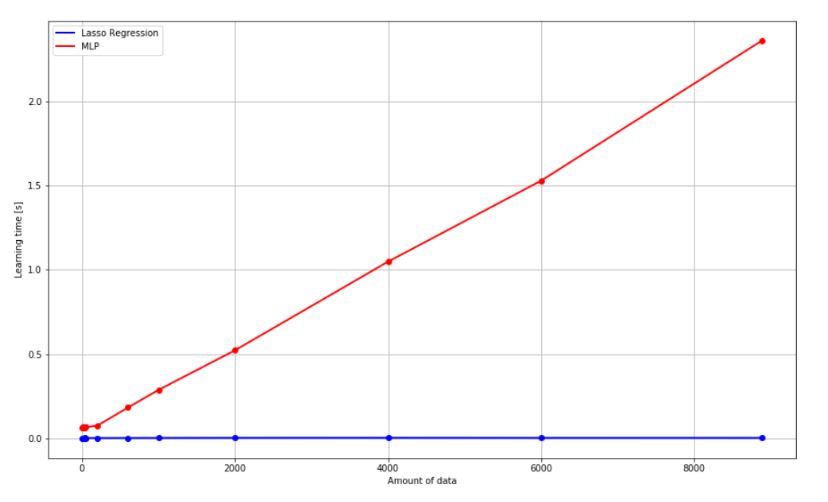
2.3 Czas uczenia algorytmów w funkcji ilości danych uczących (pokazywanych punktów z wykresu 2.1)

Podsumowanie

Na przykładzie klasyfikacji obrazów ze zbioru MNIST pokazaliśmy jedną z różnic pomiędzy klasycznym algorytmem uczenia maszynowego a uczeniem głębokim.

Głębokie sieci potrafią polepszyć swoje działanie wraz ze wzrostem ilości danych w przeciwieństwie do typowych algorytmów, które przy pewnym poziomie ilości danych osiągają nasycenie i nie poprawiają swojego działania.

Na przykładzie regresji chcieliśmy pokazać, że użycie sieci neuronowej nie zawsze jest najlepszym rozwiązaniem.

W przypadku prostych problemów mniej skomplikowane modele uzyskują dobre rezultaty na mniejszej ilości danych oraz w krótszym czasie.

Nawet stosunkowo prosta sieć neuronowa potrzebowała kilka rzędów wielkości więcej danych aby uzyskać ten sam poziom błędu.