Możliwość tworzenia prognoz bazując na danych historycznych to zdecydowanie przewaga konkurencyjna. Może być użyteczne aby zaprognozować wartości sprzedaży w celu optymalizacji stanów magazynowych jak i na przykład to predykcji cen surowców, celem optymalizacji kosztów produkcji.

W poprzednim artykule poznaliśmy kilka metod służących analizie i zrozumieniu zachowań szeregu czasowego. W drugim wpisie poświęconym szeregom czasowym przyjrzymy się bliżej modelom ARMA, ARIMA i SARIMAX służącym do modelowania i predykcji przyszłych wartości szeregu.

Jak zamodelować szereg czasowy?

Zanim przystąpimy do analizowania budowy modeli zastanówmy się co podpowiada nam intuicja. Pomyślmy o szeregu czasowym składającym się z zapisywanej co miesiąc wartości wyprodukowanych przez fabrykę samochodów - Y. X będzie oznaczało wszystkie zamówienia złożone w danym miesiącu. Z to pozostałe czynniki, na przykład przestój spowodowany chwilową awarią zasilania.

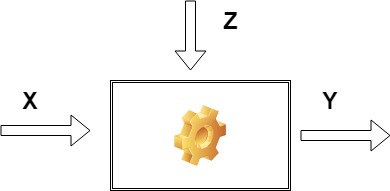
Dość logiczne wydaje się, że wartość wyprodukowanych samochodów w kolejnym miesiącu zależeć będzie od ilości złożonych w tym miesiącu zamówień. Co jednak z samochodami zamówionymi pod koniec poprzedniego miesiąca lub zleceniami których wykonanie potrwa dłużej niż miesiąc? Możemy spodziewać się że także one będą miały wpływ na wartość naszego szeregu w przyszłej chwili czasowej. Możemy również założyć, że wartość Y w danym miesiącu będzie w pewien sposób zależała od wartości w miesiącach poprzednich. Spodziewamy się, że fabryka mająca wiele zamówień w niedalekiej przeszłości będzie raczej dobrze radziła sobie również w ciągu najbliższych kilku miesięcy. Najprostsze podejście to liniowa zależność wyjścia od poprzednich wyjść i wejść. W matematycznej postaci zapiszemy to w ten sposób:

Y_[n] = α₀*X_[n] + α₁*X_[n-1] + … + α_k*X_[n-k] + b₁*Y_[n-1] + … + b_k*Y_[n-k] + E(Z)

Nie zapominajmy o losowym czynniku Z, który generuje pewną losową wartość "błędu" - E. zakładamy, że ma ona niewielki wpływ na wyjście, jednak może być to równie dobrze pożar wyłączający produkcję na kilka miesięcy. Jest to pierwszy z naszych modeli. Nazywany ARMA, składa się z dwóch części, z angielskiego: autoregressive i moving-average czyli autoregresyjnej i średniej kroczącej. Odpowiadającej kolejno części związanej z poprzednimi wyjściami czyli wartością produkcji w poprzednich miesiącach (Y_[n-1], …, Y_[n-w]) oraz z wejściami czyli zamówieniami (X_[n], …, X_[n-k]). Z postaci wzoru należy się spodziewać, że trzeba będzie nie tylko znaleźć wartości współczynników, co zrobi za nas komputer, ale również wybranie ilości uwzględnionych poprzednich kroków czasowych. Innymi słowy jak daleko sięga `pamięć`. W przypadku wejść można to zinterpretować jako maksymalna długość (w miesiącach) realizacji zamówień.

ARMA a niestacjonarność

Model ARMA nie sprawdza się jednak w przypadku szeregów niestacjonarnych. Pojęcie to poznaliśmy w poprzednim wpisie, przypomnę jednak, że szereg stacjonarny to taki który ma niezależną od czasu wartość średnią, wariancję oraz autokorelację. Niestacjonarność może mieć wiele przyczyn i nie ma jednego sposobu na pozbycie się jej, jest jednak kilka typowych przypadków w których umiemy to zrobić. Na przykład jeżeli niestacjonarność spowodowana jest trendem czy sezonowością. W poprzednim wpisie poznaliśmy jedną z metod pozbywania się trendu polegającą na obliczeniu różnic szeregu. Możemy jednak uwzględnić trend w modelu za pomocą dodatkowego składnika “I” od “integrated” czyli wprowadzeniu całkowania (a tak naprawdę operacji przeciwnej czyli różniczkowania) do modelu ARMA czy już teraz ARIMA. Podobny zabieg stosowaliśmy aby pozbyć się trendu z niestacjonarnego szeregu w poprzednim wpisie. Ostatni model - SARIMAX rozbudowywuje poprzednie poprzez uwzględnianie sezonowości.

Poznaliśmy już minimum teoretyczne czas więc na trochę praktyki. Przede wszystkim mamy do dobrania kilka parametrów. Dla modelu ARIMA są to: p - ilość poprzednich wyjść (Y), q - ilość poprzednich wejść (X), i - ilość różniczkowań. Sztuka polega na tym aby dobrać odpowiednią ilość uwzględnianych poprzednich kroków czasowych dla X i Y oraz I. Można wypróbować wszystkie modele o parametrach p, q oraz i zmieniających się na przykład od 0 do 5 i wybrać najlepszy z nich.

Autokorelacja

Sporo wiedzy możemy wyciągnąć jednak już z funkcji autokorelacji przedstawionej w poprzednim wpisie i blisko z niej spokrewnionej autokorelacji cząstkowej. Jeżeli szereg jest stacjonarny to według metody Box-Jenkinsa jeżeli funkcja autokorelacji zanika w nieskończoność za to autokorelacja cząstkowa zanika po “p” krokach mamy do czynienia z modelem AR o “p” opóźnieniach - q oraz i są wtedy równe zero. W jeżeli to autokorelacja zanika po “q” elementach za to druga funkcja zanika dopiero “w nieskończoności” mamy do czynienia z modelem MA o “q” elementach. Oczywiście nie są to jedyne dwie możliwości, jeżeli żaden z tych przypadków nie jest spełniony metoda Boxa-Jenkinsa nie daje nam odpowiedzi. Oznacza to, że jeżeli zarówno p i q zanikają w nieskończoności lub po pewnej ustalonej ilości kroków powinniśmy spróbować z pełnym modelem ARMA, ARIMA lub SARIMAX. Oczywiście może się okazać, że one również nie pasują. Zakładaliśmy przecież, że wyjście zależy liniowo od poprzednich wyjść i wejść. Pamiętajmy, że to tylko modele a sam szereg może być znacznie bardziej skomplikowany na przykład zawiera silne zależności kwadratowe i żadne z zaproponowanych przybliżeń nie będzie wystarczające.

Wpływ parametrów na dopasowanie - interaktywny przykład

Przypomnijmy sobie jeden z przebiegów z poprzedniego artykułu i spróbujmy dopasować do niego model. Jako wskaźnik jakości dopasowania wybieramy RMSE czyli sumę podniesionych do kwadratu różnic pomiędzy wartościami rzeczywistymi a przewidzianymi przez model. Czym mniejsza suma błędów tym lepiej dopasowany model.

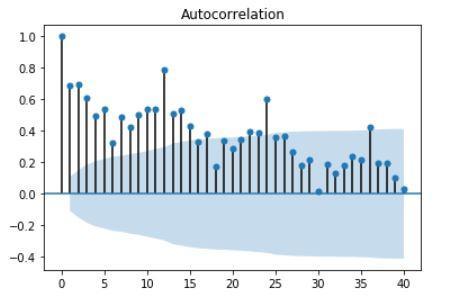
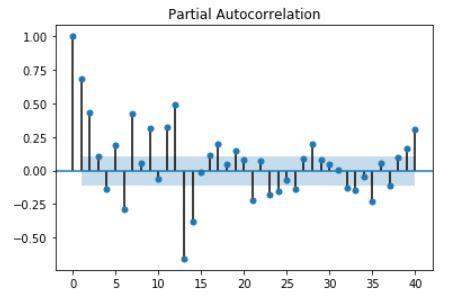
Z funkcji korelacji, co wiemy z poprzedniego wpisu, możemy odczytać że przebieg dalej posiada wyraźną sezonowość. Nie możemy też skorzystać wprost z metody Boxa-Jenkinsa. Próbki zbierane były co miesiąc więc sezonowość - wyraźna korelacja co 12 próbek, ma charakter roczny. Sugeruje to użycie modelu SARIMAX. Dla porównania przedstawimy także wyniki z modelu ARIMA nieuwzględniającego sezonowości.

W tym przypadku zwiększenie rzędu (a więc uwzględnienie większej liczby poprzednich wartości) polepszyło jakość modelu. Oczywiście, ze względu na to, że są to prawdziwe dane na wartość których wpływa ogromna liczba czynników nigdy nie uda się idealnie dopasować krzywej. Powinniśmy mieć to cały czas w pamięci modelując (a więc zakładając, pewne uproszczenia) nie tylko szeregi czasowe ale każdy inny rodzaj danych. Jak pokazaliśmy dużo jednak zależy od wybranego modelu. W tym przypadku pominięcie sezonowości spowodowało znaczne pogorszenie otrzymanych predyktorów.

Wpis ten miał za zadanie przybliżyć Ci podstawowe modele służące do przewidywania zachowań szeregów czasowych. Przedstawiłem podstawowe modele oraz połączenie pomiędzy nimi a funkcją autokorelacji. Po obu artykułach mając już podstawową wiedzę o właściwościach, analizie i modelowaniu szeregów czasowych chciałbym zachęcić Cię do własnych prób z pozostałymi przebiegami ze zbioru danych przedstawionego w poprzednim artykule z tego cyklu.